Day: 05.12.2025

1․ 4a(3a−5)=4ax3a=12a²-4ax5=12a²-20a

2․ −2x(7x+9)=-2x.7x-2x.9=14x²-18x

3․ 5m2(2m2−3m+4)=5m².2m².3m+4=10m^4-15m²+4

4․ −6p(4p3−p2+2p−1)=6p.4p²p

5. 3×3(5x−7×2+6)

6. −8k2(3k2+2k−4)

7. 7y(4y2−y+5)

8. −3t3(t2−6t+9)

9. 2n(9n3−3n+1)

10. 5q2(2q−4q2+7)

11․ (2x+3)(x+5)

12․ (a−4)(3a+2)

13․ (m+7)(m2−3m+1)

14․ (2p−3q)(4p+q)

15․ (x2+2x−1)(x−3)

16․ (-3a)(-5b)

17․ (−4x)(7xy)

18․ (6m2)(−2m3)

19․ (−8k2)(−3k)

20․ (5p3q)(−4pq2)

21․ (−2x2y)(−3x3y4)

22․ (7a2b3)(−a3b)

23․ (−9m4n)(−m2n3)

24․ (12x)(−x2y3)

25․ (−5p2q4)(4p3q)

Լրացուցիչ աշխատանք

Միանդամի և բազմանդամի արտադրյալը մի բազմանդամ է, որի անդամներն են այդ միանդամի և բազմանդամի բոլոր անդամների արտադրյալները:

Օրինակ՝ բազմապատկենք a միանդամը և a+b բազմանդամը: Ստանում ենք՝ a⋅(a+b)=a2+ab:

Հիշենք, որ միանդամը բազմանդամով բազմապատկելիս ստանում ենք բազմանդամ:

Եթե վերևի օրինակի հավասարությունը գրենք հակառակ կարգով, ապա նկատում ենք, որ a2+ab բազմանդամը ներկայացվում է a միանդամի և a+b բազմանդամի արտադրյալի տեսքով՝ a2+ab=a(a+b):

Այս գործընթացը անվանում են ընդհանուր արտադրիչը փակագծերից դուրս բերում: Մեր օրինակում փակագծերից դուրս է բերվել a ընդհանուր արտադրիչը:

Ահա ընդհանուր արտադրիչը փակագծերից դուրս բերման ևս մեկ օրինակ

՝3x3y−x2y2=x2y(3x−y)

Առաջադրանքներ․

1)Գտեք միանդամի և բազմանդամի արտադրյալին հավասար բազմանդամը․

3 և (a+b)

3a+3b

x և (a-b)

ax-ab

(x+1) և 5

5x+5

(a-b) և x

ax-bx

2)Գտեք միանդամի և բազմանդամի արտադրյալին հավասար բազմանդամը

․(-2)(x+y)

-2x-2y

(7+3y-x2y)(-2xy)

-14xy-6y+2x³y²

(-abc)(ab+ac+bc)

-a²b²c-a²bc²-ab²c²

-ac(a+2c)

-a²c-2ac²

3)Ձևափոխեք արտահայտությունը կատարյալ տեսքի բազմանդամի․

2(a+b)+4(a+b)=2ab+4ab

4(x-y)+7(x-y)=

4-2(x+1)=

2ab(a+2b)-3ab2 (a-4)=

Առաջադրանքներ․

1)54 սմ հիմքով հավասարասրուն եռանկյան մեջ տարված է ABC անկյան կիսորդը: Օգտագործելով եռանկյունների հավասարության երկրորդ հայտանիշը` ապացուցիր, որ BD հատվածը հանդիսանում է միջնագիծ և որոշիր AD հատվածի երկարությունը:

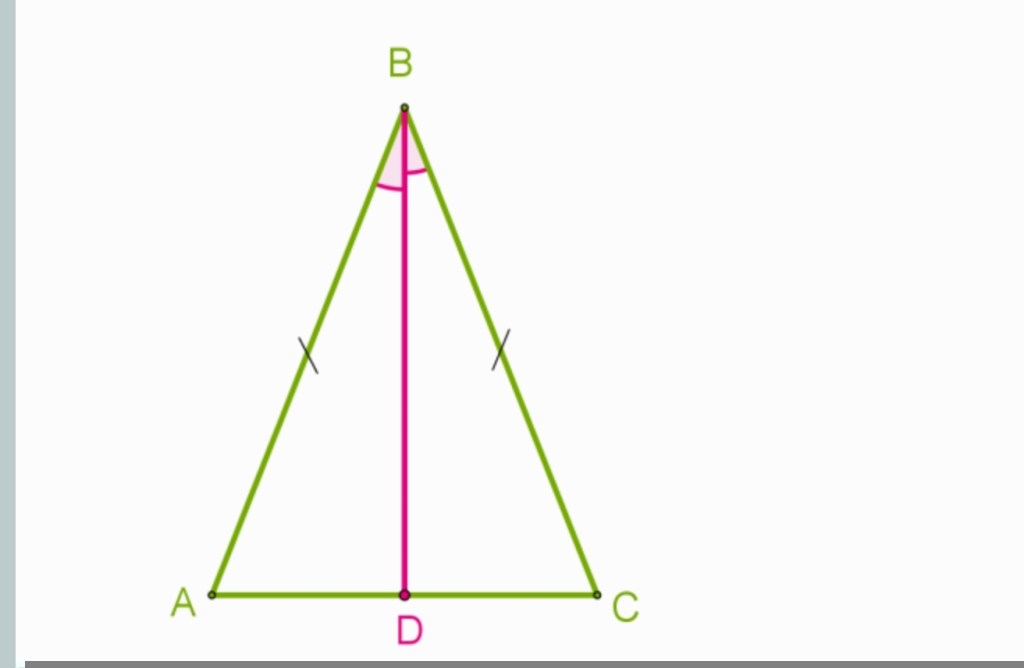
Դիտարկենք եռանկյունի ABD և եռանկյունի DBC: Քանի որ մեր եռնկյունին հավասարասյուն է, ապա AB=BC, անկյուն A= անկյունC, անկյուն ABD= անկյուն DBC (քանի որ BD հանդիսանում է կիսորդ)։ Ապա ըստ եռանկյունների հավասարության երկրորդ հայտանիշի եռանկյունի ABD =DBC: Հետևաբար => AD=DC, ուրեմն D միջնակետ է, իսկ BD միջնագիծ։

AD=54:2=27 սմ

2)AB և CD հատվածները հատվում են AB հատվածի O միջնակետում, <OAD=<OBC:

ա)Ապացուցեք, որ ΔCBO = ΔDAO

բ)Գտեք BC-ն և CO-ն, եթե CD=26 սմ, AD=15սմ

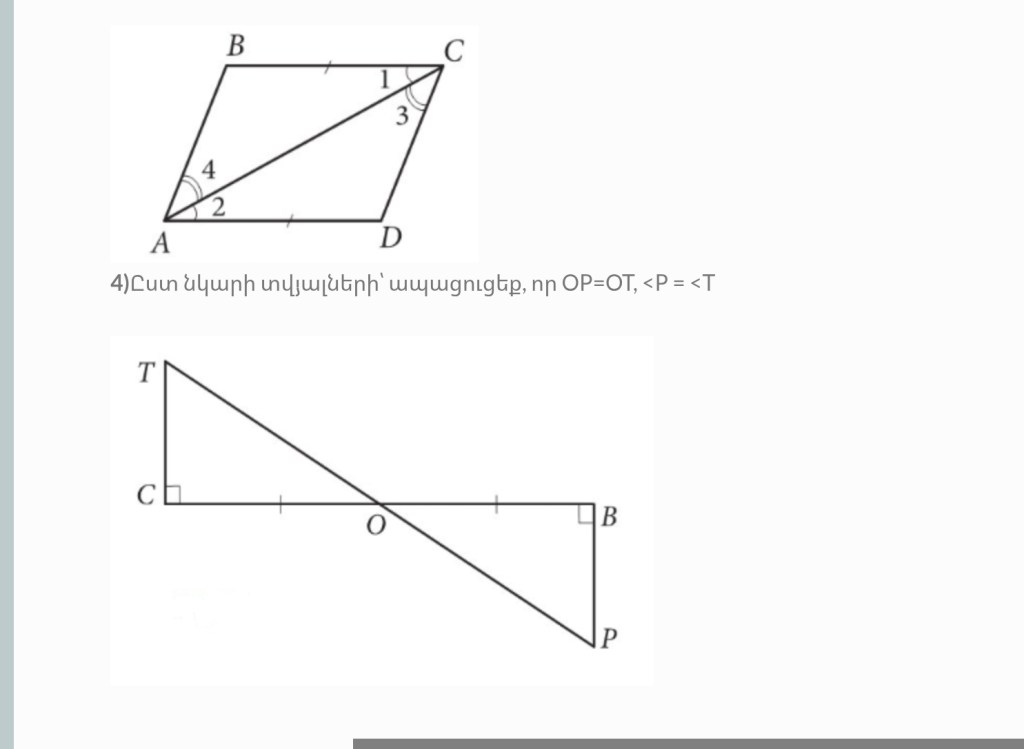
3)Տրված է <1 = <2, < 3 = <4:

ա)Ապացուցեք, որ ΔABC = ΔCDA:

բ)Գտեք AB-ն և BC-ն, եթե AD=19 սմ, CD=11 սմ: