Category: Երկրաչափություն 7

Առաջադրանքներ․

1)54 սմ հիմքով հավասարասրուն եռանկյան մեջ տարված է ABC անկյան կիսորդը: Օգտագործելով եռանկյունների հավասարության երկրորդ հայտանիշը` ապացուցիր, որ BD հատվածը հանդիսանում է միջնագիծ և որոշիր AD հատվածի երկարությունը:

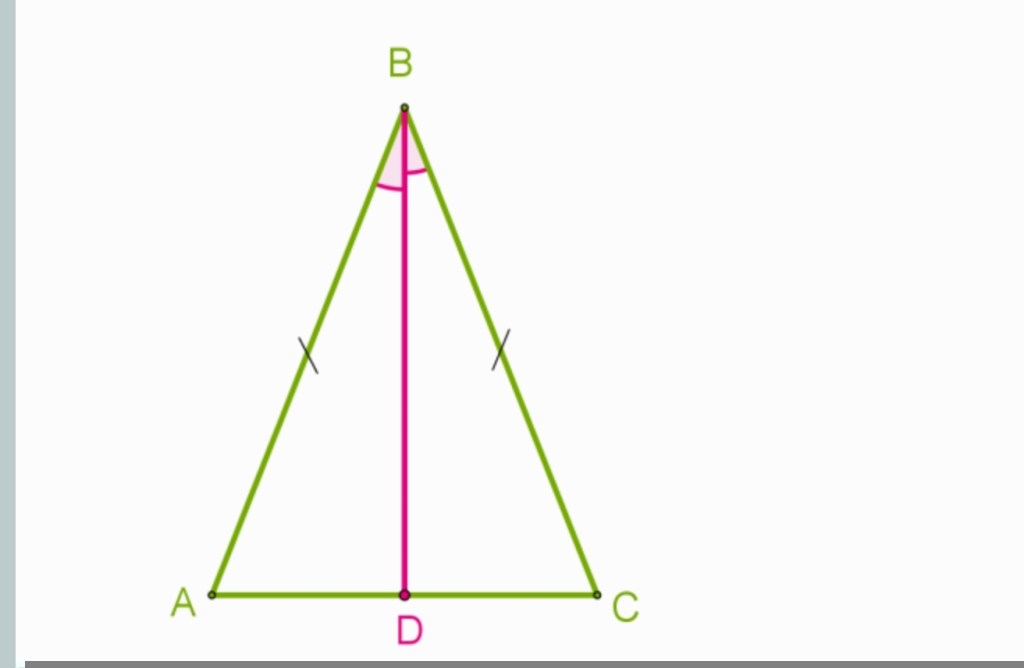
Դիտարկենք եռանկյունի ABD և եռանկյունի DBC: Քանի որ մեր եռնկյունին հավասարասյուն է, ապա AB=BC, անկյուն A= անկյունC, անկյուն ABD= անկյուն DBC (քանի որ BD հանդիսանում է կիսորդ)։ Ապա ըստ եռանկյունների հավասարության երկրորդ հայտանիշի եռանկյունի ABD =DBC: Հետևաբար => AD=DC, ուրեմն D միջնակետ է, իսկ BD միջնագիծ։

AD=54:2=27 սմ

2)AB և CD հատվածները հատվում են AB հատվածի O միջնակետում, <OAD=<OBC:

ա)Ապացուցեք, որ ΔCBO = ΔDAO

բ)Գտեք BC-ն և CO-ն, եթե CD=26 սմ, AD=15սմ

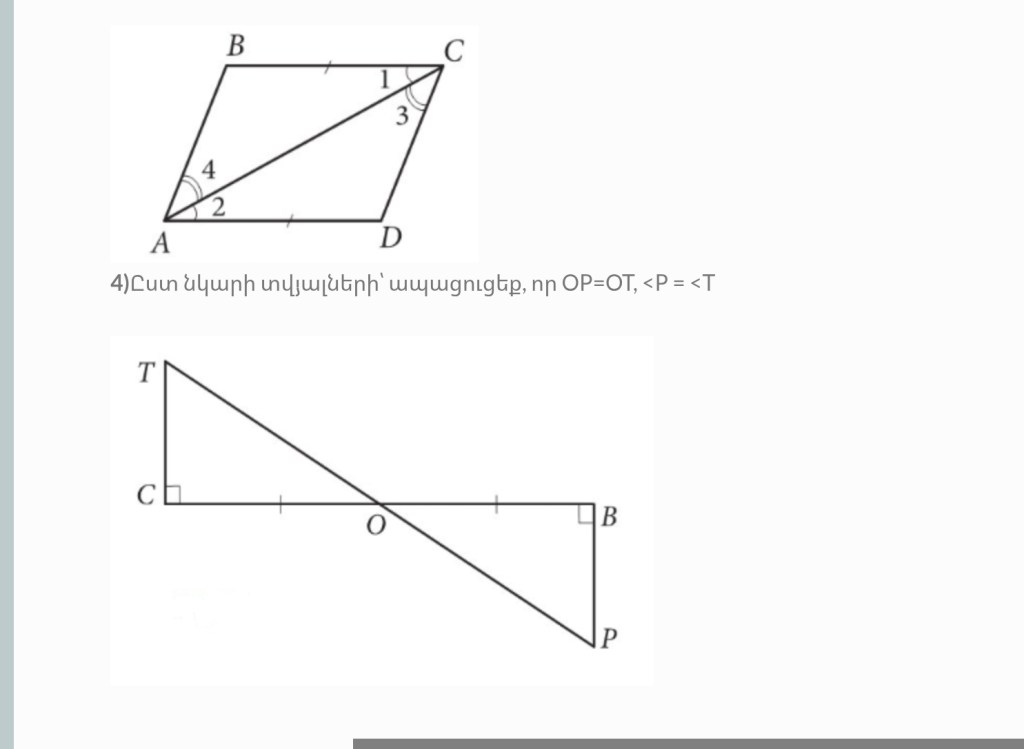
3)Տրված է <1 = <2, < 3 = <4:

ա)Ապացուցեք, որ ΔABC = ΔCDA:

բ)Գտեք AB-ն և BC-ն, եթե AD=19 սմ, CD=11 սմ:

117․ A և C կետերը գտնվում են a ուղղի միևնույն կողմում։ a ուղղին տարված AB և CD ուղղահայացները հավասար են։ա) Ապացուցեք, որ ΔABD = ΔCDB,

ΔABD=ΔCBD

AB=CD

∠ABD=∠CDB=90°

բ) Գտե՛ք ∠ABC-ն, եթե ∠ADB = 44°:

120․ Բութանկյուն հավասարասրուն եռանկյան պարագիծը 45 սմ է, իսկ նրա կողմերից մեկը մյուսից փոքր է 9 սմ–ով։ Գտեք եռանկյան կողմերը։

121. BC հիմքով ABC հավասարասրուն եռանկյան պարագիծը 40 սմ է, իսկ BCD հավասարակողմ եռանկյան պարագիծը 45 սմ: Գտեք AB և BC կողմերը։

Լրացուցիչ աշխատանք

118․ ABC եռանկյան AD միջնագիծը շարունակված է BC-ի մյուս կողմում DE հատվածով, որը հավասար է AD-ին, իսկ E կետը միացված է C կետին:ա) Ապացուցեք, որ ΔABD = ΔECD,բ) գտեք ∠ACE-ն, եթե ∠ACD = 56°, ∠ABD = 40°:

119․ Հավասարասրուն եռանկյան հիմքը երկու անգամ փոքր է սրունքից, իսկ պարագիծը 50 սմ է։ Գտեք եռանկյան կողմերը:

Առաջադրանքներ․

1.Ճիշտ ընտրիր ALM եռանկյան կողմերի և անկյունների անվանումները:

ա) ∡M անկյան հանդիպակաց կողմը՝

AL✓

LM

MA

բ) LM կողմի հանդիպակաց անկյունը՝

∡M

∡L

∡A✓

գ) AL կողմին առընթեր անկյունները

՝∡M;∡A

∡L;∡M

∡A;∡L✓

2.Տրված է ուղղանկյուն:ծ Արդյո՞ք GOF և HOE եռանկյունները հավասար են՝ եռանկյունների հավասարության առաջին հայտանիշի համաձայն: Հիմնավորիր:

Քանի որ ուղղանկյան անկյունագծերը հատվում են և հատման կեսում կիսվում են, ապա կասենք որ EO=OG, HO=OF, իսկ անկյուն ∡EOH= ∡FOG(որպես հակադիր անկյուններ) Ըստ եռանկյունների հավասարության առաջին հայտանիշի ΔGOF=ΔHOE:

3. O հատման կետը AG և LV հատվածների միջնակետն է:

Գտիր ∡A և ∡L անկյունների մեծությունները ALO եռանկյան մեջ, եթե ∡V=24° և∡G=33°

Քանի որ հատվածները կիսվում են, ապա՝

ա)ALO եռանկյան LO կողմը հավասար է GVO եռանկյան OV կողմին:

բ)ALO եռանկյան AO կողմը հավասար է՝ OG կողմին:

LOA անկյունը հավասար է ……………. անկյանը՝ որպես հակադիր անկյուն:

Եռանկյունները հավասար են եռանկյունների հավասարության առաջին հայտանիշի համաձայն:

Հավասար եռանկյունների համապատասխան անկյունները հավասար են՝

∡A=

∡L=

առաջադրանք

Դասարանական առաջադրանքներ

Կից անկյուններից մեկը ուղիղ է։ Սո՞ւր, ուղի՞ղ, թե՞ բութ է մյուս անկյունը:

Բութ։

Արդյոք ճշմարի՞տ է հետևյալ պնդումը, եթե կից անկյունները հավասար են, ապա դրանք ուղիղ անկյուններ են:

Այո։

Տրված են երկու հավասար անկյուններ: Հավասար ե՞ն, արդյոք, դրանց կից անկյունները։

Այո։

Գտե՛ք hk և kl կից անկյունները, եթե՝

ա) ∠hk-ն 40°-ով փոքր է ∠kl-ից, —

բ) ∠hk-ն 120°-ով մեծ է ∠kl-իg,

գ) ∠hk-ն 47°18′-ով մեծ է ∠kl-ից,

դ) ∠hk = 3∠kl

,ե) ∠hk : ∠kl = 5 : 4:

O կետից տարված են OA, OB և OC ճառագայթները, ընդ որում` BO⊥AO (նկ. 49): AOB և BOC անկյունների կիսորդներով կազմված անկյունը 20° է։ Գտեք BOC և AOC անկյունները

։Տնային աշխատանք

72․ O կետից տարված են OA, OB և OC ճառագայթները, ընդ որում՝ OB⊥OA (նկ. 50): AOB և BOC անկյունների կիսորդներով կազմված անկյունը 75° է։ Գտեք BOC և AOC անկյունները։

1) Քանի՞ աստիճանով է պտտվում ժամացույցի րոպեասլաքը 5 րոպեում:

30°

2) Քանի՞ աստիճանով է պտտվում ժամացույցի ժամսլաքը 2 ժամում:

3) Կառուցել MNK և CNK անկյուններն այնպես, որ ∠MNK = 130°, ∠CNK = 80° և NC ճառագայթը MNK անկյունը բաժանի երկու մասի։ Գտնել MNC անկյան աստիճանային չափը։

50°

4) Փռված անկյան ո՞ր մասն է կազմում 70օ-ի անկյունը:

5) Ուղիղ անկյան ո՞ր մասն է կազմում 42°-ի անկյունը:

6) OE Ճառագայթը AOB անկյունը տրոհում է երկու անկյան: Գտեք ∠AOB-ն, եթե՝

ա) ∠AOE=440, ∠EOB=770,

բ) ∠AOE=12037’, ∠EOB=108025’:

Առաջադրանք 18

OB\OA

OC/OA

OB/OC

Առաջադրանք 19

OA=OB

OA<AB

Առաջադրանք 20

ա) B-կետը AC կետերի միջակետն է։

C-կետը BD կետերի միջակետն է։

D-կետը CE կետերի միջակետն է։

բ) D-կետը CE կետերի միջակետն է։

գ) C-կետը BD կետերի միջակետն է։

Լուծում