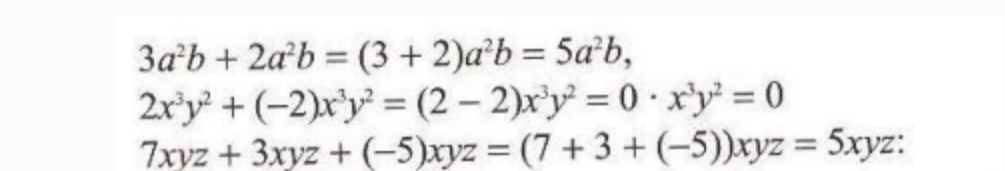Եթե թվային արտահայտության մեջ մտնող որոշ թվեր (կամ բոլորը) փոխարինվեն տառերով (տարբեր թվերը՝ տարբեր տառերով), ապա կստացվի տառային արտահայտություն:
Ավելի հաճախ օգտագործում են լատինական այբուբենի տառերը։
ՕՐԻՆԱԿ 1.
Եթե (5 + 3)/2 թվային արտահայտության մեջ 5 թիվը փոխարինենք a տառով, 3 թիվը` b տառով և 2 թիվը c տառով, ապա կստանանք (a+b)/c տառային արտահայտությունը:
Խնդիրներ ձևակերպելիս թվերի փոխարեն սովորաբար կիրառում են լատիներեն տառեր՝ a,b,c,d։ Հաճախ անհայտ մեծությունները գրում են x տառի միջոցով, s-ով ընդունված է նշանակել ճանապարհի երկարությունը (օրինակ՝ մեքենայի անցած), m-ով՝ առարկայի զանգվածը, t-ով՝ ժամանակը:
Օրինակ 2․
Մատիտն արժե 40 դրամ, իսկ գրիչը՝ 100 դրամ:
Եթե օրինակում մեզ հայտնի չլինեն մատիտների և գրիչների գները, ապա կարող ենք դրանք գրել տառերի միջոցով: Օրինակ՝ դիցուք մեկ մատիտն արժե x դրամ, իսկ գրիչը՝ y դրամ: Երկու մատիտը և չորս գրիչները միասին կարժենան 2⋅x+4⋅y դրամ:
Տառային արտահայտությունները երբեմն օգտագործում են տեքստային խնդիրներ լուծելիս։ Ընդ որում խնդրի լուծումը տառային արտահայտություն կազմելով հաճախ անվանում են խնդրի լուծում ընդհանուր տեսքով: Այս հնարանքը հաճախ օգտագործում են երկրաչափության և ֆիզիկայի մեջ։ Տառային արտահայտությունները կիրառվում են բանաձևեր գրառելիս։
Բանաձևը մաթեմատիկական և այլ օրենքների գրառումն է տառային արտահայտությունների միջոցով։
Որոշ բանաձևերի մենք արդեն ծանոթ ենք:
Օրինակ՝
1) P = 2(a + b) — դա a և b կողմերով ուղղանկյան պարագծի բանաձևն է,
2) S = ab -ն a և b կողմերով ուղղանկյան մակերեսի բանաձևն է,
3) V = abc -ն a, b, c չափումներն ունեցող ուղղանկյունանիստի ծավալի բանաձևն է,
4) S = vt -ն հավասարաչափ շարժման դեպքում անցած ճանապարհի բանաձևն է, որտեղ v-ն շարժման արագությունն է, իսկ t-ն ժամանակը,
5) P = 4a -ն a կողմով քառակուսու պարագծի բանաձևն է,
6) S = a2 -ն a կողմով քառակուսու մակերեսի բանաձևն է:
Տառային արտահայտությունները անվանում են նաև հանրահաշվական արտահայտություններ, թվերը նույնպես անվանում են հանրահաշվականարտահայտություններ:
Եթե տված երկու հանրահաշվական արտահայտություններ միացնենք գումարման, հանման, բազմապատկման կամ բաժանման գործողություններով, ապա նորից կստանանք հանրահաշվական արտահայտություն, որը համապատասխանաբար անվանում են տված հանրահաշվական արտահայտությունների գումար, տարբերություն, արտադրյալ կամ քանորդ: Իհարկե, ոչ բոլոր երկու արտահայտությունների համար կարելի է սահմանել նրանց քանորդը։ Դա կապված է 0-ի վրա բաժանելու անթույլատրելիության հետ։Օրինակ՝ a + 1 և a — b երկու հանրահաշվական արտահայտությունների գումարը, տարբերությունը, արտադրյալը և քանորդը հետևյալ տեսքերն ունեցող հանրահաշվական արտահայտություններն են`
(a + 1) + (a — b).
(a + 1) — (a — b)
(a + 1)(a — b)
(a + 1) / (a — b) կամ (a + 1) ։ (a — b)
Բազմապատկման նշանը հաճախ բաց են թողնում։
Օրինակ՝ (a + 1) * (a — b) արտադրյալը գրառում են այսպես` (a + 1)(a — b)
Դասարանական աշխատանք
1․ Տրված թվային արտահայտության մեջ 5-ը փոխարինեք a-ով և գրեք ստացված տառային արտահայտությունը.
ա) 7 * 5 -1=7a-1
բ) 2 * 5 — 5 : 3=2a — a:3
2․ Բերեք տառային արտահայտությունների օրինակներ:
a2+9=9a
81 + h = 2 — 1
3․ a + 3 տառային արտահայտության մեջ a տառի փոխարեն տեղադրեք հետևյալ թիվը.
ա) 5
բ) 3= 3+3
գ) 1= 1+3
դ) 0= 0+3
ե)-1= -1+3
զ) -3: -3+3
4․ a + 2 արտահայտությունը a-ի և 2-ի գումարն է, 3 — x արտահայտությունը 3-ի և x — ի տարբերությունն է: Դրանց օրինակով կարդացեք արտահայտությունը.
ա) 5 + a= 5-ի և a-ի գումարը
բ) 7 — a= 7-ի և a-ի տարբերությունը
գ) 4 — x= 4-ի և x-ի տարբերությունը
դ) a + 12= a-ի և 12-ի գումարը
ե) 2a,= 2-ի և a-ի արտադրյալը
զ) 7b,= 7-ի և b-ի արտադրյալը
է) — 3a= -3ի և a-ի արտադրյալը
ը) a+ (- 3) : = a-ի և (-3)-ի գումարը։
5․ Օգտվելով բերված նմուշօրինակից` հաշվեք տրված տառային արտահայտության արժեքը.
ա) 10 — 4x, երբ x = — 5
Լուծում: Երբ x = — 5, ապա 10 — 4x = 10 — 4 * (- 5) = 10 + 20 = 30
բ) 2x + 1, երբ x = 511
գ) 6 + 8x, երբ x = — 1-2
դ) 5 — 4a, երբ a = 2-40
ե) 3 — 7b, երբ b = — 211
Լրացուցիչ աշխատանք
1․ Գտեք 7 + x տառային արտահայտության արժեքը, երբ x-ը հավասար է.
ա) 0=7 + 0 =7
բ) -4=7 + (-4)=11
գ) 3= 7+3 =10
դ) -7 = 7 + (-7) = 0
ե)-1 = 7 + (-1) = -8
զ)-10 = 7 + ( — 10) = -17
2․ Գտեք տառային արտահայտության արժեքը
ա) a + b, երբ a = 1, b = 3
1+3=5
բ ) 2x — y, երբ x = 5, y = 6
2 x 5 =10
10 — 6 =4
գ) a — b, երբ a = — 2, b = 4
(-2) — 4= -6
դ) 3x — 2y, երբ x = — 1, y =4:
3 x (-1) =-3
2 x 4= 88 — (-1) =9
ե) ab, երբ a = 3/4, b = 1 3/5
1 1/5
զ) 2(a + b), երբ a = 3/10, b = 1 1/2
3 3/5
է) abc, երբ a = 1/3, b = 1 1/2, c = 2
1
3․ ա) Ծառայողի աշխատավարձը 200000 դրամ էր։ Սկզբում այն բարձրացրին 30%-ով։ Որոշ ժամանակ անց նոր աշխատավարձը բարձրացրին ևս 20%-ով։ Որոշեք ծառայողի վերջնական աշխատավարձը:
260. 000 + 52 000 = 312. 000
բ) Ապրանքի գինը 3000 դրամ էր։ Սկզբում այն իջեցրին 20%-ով։ Որոշ ժամանակ անց ստացված նոր գինը իջեցրին ևս 10%-ով։ Որոշեք ապրանքի վերջնական գինը։
2400 — 240 = 2160